Module 18 1-Sample t-Test

Prior to this module, hypothesis testing methods required knowing σ, which is a parameter that is seldom known. When σ is replaced by its estimator, s, the test statistic follows a Student’s t rather than a standard normal (Z) distribution. In this module, the t-distribution is described and a 1-Sample t-Test for testing that the mean from one population equals a specific value is discussed.

18.1 t-distribution

A t-distribution is similar to a standard normal distribution (i.e., N(0,1)) in that it is centered on 0 and is bell shaped (Figure 18.1). The t-distribution differs from the standard normal distribution in that it is heavier in the tails, flatter near the center, and its exact dispersion is dictated by a quantity called the degrees-of-freedom (df). The t-distribution is “flatter and fatter” because of the uncertainty surrounding the use of s rather than σ in the standard error calculation.66 The degrees-of-freedom are related to n and generally come from the denominator in the standard deviation calculation. As the degrees-of-freedom increase, the t-distribution becomes narrower, taller, and approaches the standard normal distribution (Figure 18.1).

 

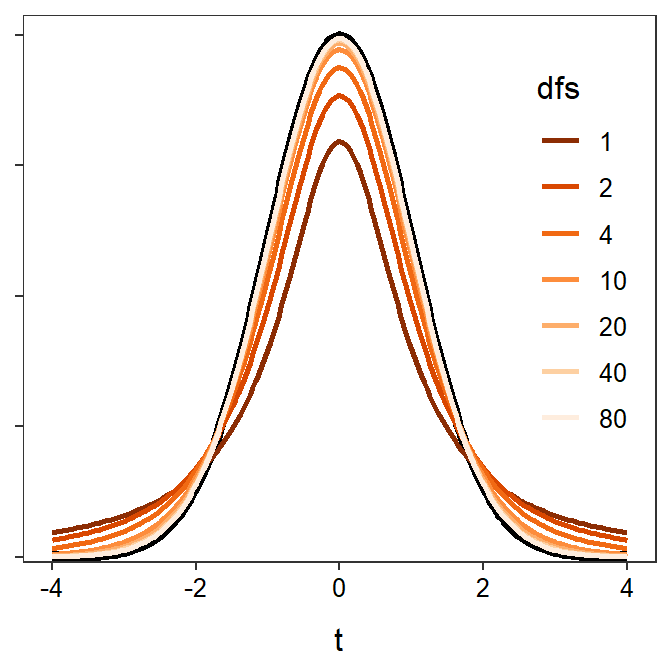
Standard normal (black) and t-distributions with varying degrees-of-freedom.

Figure 18.1: Standard normal (black) and t-distributions with varying degrees-of-freedom.

 

Proportional areas on a t-distribution are computed using distrib() similar to what was described for a normal distribution in Modules 6 and 11. The major exceptions for using distrib() with a t-distribution is that distrib="t" must be used and the degrees-of-freedom must be given in df= (how to find df is discussed in subsequent sections). For example, the area right of t=-1.456 on a t-distribution with 9 df is 0.9103 (Figure 18.2).

( distrib(-1.456,distrib="t",df=9,lower.tail=FALSE) )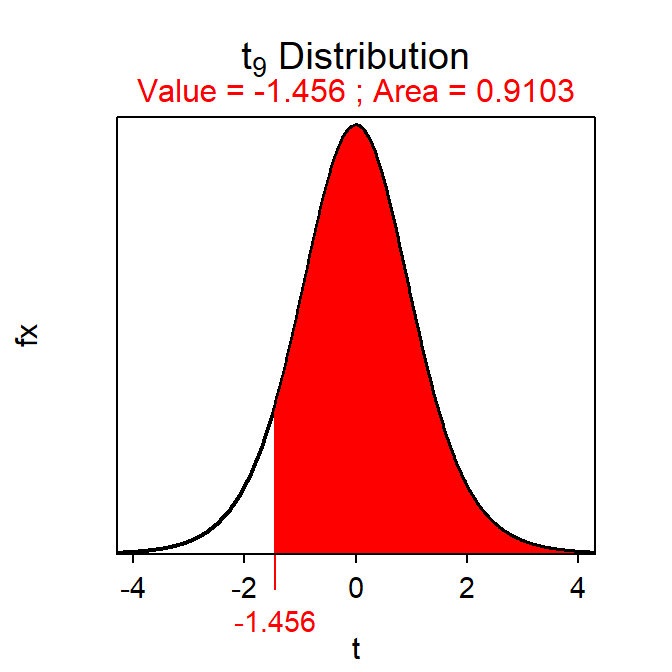
Depiction of the area to the right of t=-1.456 on a t-distribution with 9 df.

Figure 18.2: Depiction of the area to the right of t=-1.456 on a t-distribution with 9 df.

 

Similarly, the t with an upper-tail area of 0.95 on a t-distribution with 19 df is -1.729 (Figure 18.3).67

( distrib(0.95,distrib="t",type="q",df=19,lower.tail=FALSE) )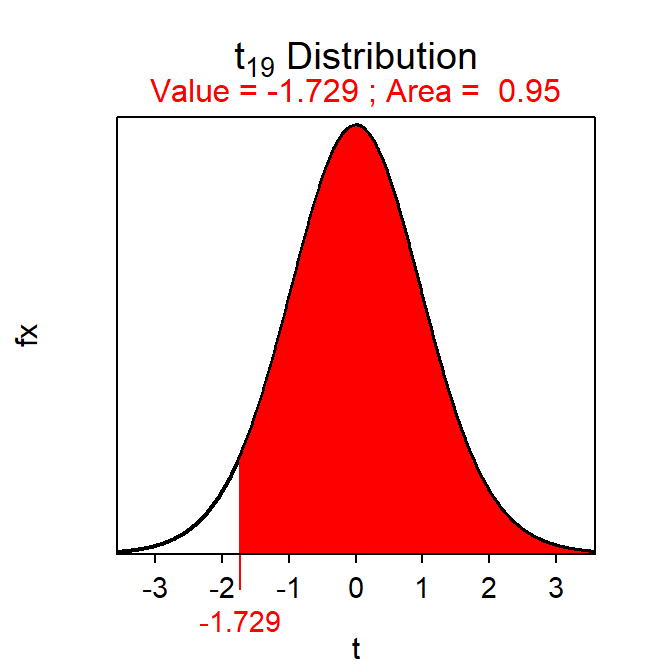
Depiction of the value of t with an area to the right of 0.95 on a t-distribution with 19 df.

Figure 18.3: Depiction of the value of t with an area to the right of 0.95 on a t-distribution with 19 df.

18.2 1-Sample t-Test Specifics

A 1-Sample t-Test is similar to a 1-Sample Z-test in that both test the same H0. The difference, as discussed above, is that when σ is replaced by s, the test statistic becomes t and the scaling factor for confidence regions becomes a t*. Other aspects are similar between the two tests as shown below.68

  • Hypothesis: H0:μ=μ0
  • Statistic: \(\bar{\text{x}}\)
  • Test Statistic: t=\(\frac{\bar{\text{x}}-\mu_{0}}{\frac{\text{s}}{\sqrt{\text{n}}}}\)
  • Confidence Region: \(\bar{\text{x}}+\text{t}^{*}\frac{\text{s}}{\sqrt{\text{n}}}\)
  • df: n-1
  • Assumptions:
    • σ is UNknown
    • n≥40, n≥15 and the sample (i.e., histogram) is not strongly skewed, OR the sample is normally distributed.
  • Use with: Quantitative response, one group (or population), σ UNknown.

18.3 Examples

18.3.1 Purchase Catch of Salmon?

Below are the 11-steps (Section 17.1) for completing a full hypothesis test for the following situation:

A prospective buyer will buy a catch of several thousand salmon if the mean weight of all salmon in the catch is at least 19.9 lbs. A random selection of 50 salmon had a mean of 20.1 and a standard deviation of 0.76 lbs. Should the buyer accept the catch at the 5% level?

  1. α=0.05.
  2. H0:μ=19.9 lbs vs. HA:μ >19.9 lbs where μ is the mean weight of ALL salmon in the catch.
  3. A 1-Sample t-Test is required because …
    1. a quantitative variable (weight) was measured,
    2. individuals from one group (or population) were considered (this catch of salmon), and
    3. σ is UNknown.69
  4. The data appear to be part of an observational study with random selection.
  5. The assumptions are met because …
    1. n=50≥40 and
    2. σ is unknown.
  6. \(\bar{\text{x}}\) = 20.1 lbs (and s = 0.76 lbs).
  7. t = \(\frac{20.1-19.9}{\frac{0.76}{\sqrt{50}}}\) = \(\frac{0.2}{0.107}\) = 1.87 with df = 50-1 = 49.
  8. p-value = 0.0337.
  9. H0: is rejected because the p-value <α.
  10. The average weight of ALL salmon in this catch appears to be greater than 19.9 lbs; thus, the buyer should accept this catch of salmon.
  11. I am 95% confident that the mean weight of ALL salmon in the catch is greater than 19.92 lbs (i.e., 20.1-1.677×\(\frac{0.76}{\sqrt{50}}\) = 20.1-0.18 = 19.92).

R Appendix:

( pval <- distrib(1.87,distrib="t",df=49,lower.tail=FALSE) )

( tstar <- distrib(0.95,distrib="t",type="q",df=49,lower.tail=FALSE) )

 

18.3.2 Body Temperature

Below are the 11-steps (Section 17.1) for completing a full hypothesis test for the following situation:

*Machowiak et al. (1992) critically examined the belief that the mean body temperature is 98.6oF by measuring body temperatures in a sample of healthy humans. Use their results in Table 18.1 to determine at the 1% level if the mean body temperature differs from 98.6oF.

Table 18.1: Descriptive statistics from measuring the body temperature of a sample of healthy humans.
n mean sd min Q1 median Q3 max
130 98.25 0.73 96.3 97.8 98.3 98.7 100.8

 

  1. α=0.01.
  2. H0:μ=98.6oF vs. HA:μ≠98.6oF, where μ is the mean body temperature for ALL healthy humans. [Note that not equals was used because the researchers want to determine if the temperature is different from \(98.6\)oF.]
  3. A 1-Sample t-Test is required because …
    1. a quantitative variable (i.e., body temperature) was measured,
    2. individuals from one group (or population) is considered (i.e., healthy humans), and
    3. σ is unknown (i.e., not given in the background).
  4. The data appear to be part of an observational study although this is not made clear in the background information. There is also no evidence that randomization was used.
  5. The assumptions are met because …
    1. n=130≥40 and
    2. σ is unknown.
  6. \(\bar{\text{x}}\) = 98.25oF.
  7. t = \(\frac{98.25-98.6}{\frac{0.73}{\sqrt{130}}}\) = \(\frac{-0.35}{0.064}\) = -5.469 with df = 130-1 = 129.
  8. p-value=0.0000002. [Note that the result of distrib() is multiplied by 2 because of the not equals HA.]
  9. Reject H0 because p-value<α=0.01.
  10. It appears that the mean body temperature of ALL healthy humans is less than 98.6oF. [Note that the test was for a difference but because \(\bar{\text{x}}\)<98.6 this more specific conclusion can be made.]
  11. I am 99% confident that the mean body temperature (μ) for ALL healthy humans is between 98.08oC (=98.25-2.614×0.064) and 98.42oC (=98.25+2.614×0.064). [Note that the area in distrib() is \(1-\frac{\alpha}{2}\) because of the not equals HA:.]

R Appendix:

( pval <- 2*distrib(-5.469,distrib="t",df=129) )

(tstar <- distrib(0.995,distrib="t",df=129,type="q") )

 

  1. Recall that the sample standard deviation is a statistic and is thus subject to sampling variability.↩︎

  2. This “reverse” calculation would be t* for a 95% lower confidence bound.↩︎

  3. Compare these specifics to those for a 1-Sample Z-test in Section 17.2.↩︎

  4. If σ is given, then it will appear in the background information to the question and will be in a sentence that uses the words “population,” “assume that,” or “suppose that.”↩︎