Introduction

We are deprecating residPlot() from the next version of FSA (v0.9.0). It will likely be removed at the end of the year 2001. We are taking this action to make FSA more focused on fisheries applications and to eliminate “black box” functions. residPlot() was originally designed for students to quickly visualize residuals from one- and two-way ANOVAs and simple, indicator variable, and logistic regressions.¹

We now feel that students are better served by learning how to create these visualizations using methods provided by ggplot2, which require more code, but are more modern, flexible, and transparent.

The basic plots produced by residPlot() are recreated here using ggplot2 to provide a resource to help users that relied on residPlot() transition to ggplot2.

The examples below require the following additional packages.

library(tidyverse)  # for dplyr and ggplot2
library(FSA)        # fitPlot() code may not run after >v0.9.0
library(patchwork)  # placing plots (in conclusion)

Most examples below use the Mirex data set from FSA, which contains the concentration of mirex in the tissue and the body weight of two species of salmon (chinook and coho) captured in six years. The year variable is converted to a factor below for modeling purposes. These same data were used in this post about depredating fitPlot().

Mirex$year <- factor(Mirex$year)
Mirex$gt2 <- ifelse(Mirex$mirex>0.2,1,0)
FSA::peek(Mirex,n=10)  # examine a portion of the data frame

##     year weight mirex species gt2
## 1   1977   0.41  0.16 chinook   0
## 14  1977   3.29  0.23    coho   1
## 27  1982   0.70  0.10    coho   0
## 41  1982   5.09  0.27    coho   1
## 54  1986   1.82  0.12 chinook   0
## 68  1986   8.40  0.13 chinook   0
## 81  1992  10.00  0.48 chinook   1
## 95  1996   5.70  0.16    coho   0
## 108 1999   5.11  0.11    coho   0
## 122 1999  11.82  0.09 chinook   0

One-Way ANOVA

The code below fits a one-way ANOVA model to examine if mean weight differs by species.

aov1 <- lm(weight~species,data=Mirex)
anova(aov1)

## Analysis of Variance Table
## 
## Response: weight
##            Df Sum Sq Mean Sq F value    Pr(>F)
## species     1  282.4 282.399  27.657 6.404e-07
## Residuals 120 1225.3  10.211

residPlot() from FSA (before v0.9.0) produces a boxplot of residuals by group (left) and a histogram of residuals (right).

FSA::residPlot(aov1)

A data.frame of the two variables used in the ANOVA appended with the fitted values and residuals from the model fit must be made to construct this plot using ggplot(). Studentized residuals are included below in case you would prefer to plot them.²

tmp <- dplyr::select(Mirex,weight,species) %>%
  dplyr::mutate(fits=fitted(aov1),
                resids=resid(aov1),
                sresids=rstudent(aov1))
peek(tmp,n=8)

##     weight species     fits     resids    sresids
## 1     0.41 chinook 6.314776 -5.9047761 -1.8814369
## 17    4.77    coho 3.257091  1.5129091  0.4762846
## 35    2.92 chinook 6.314776 -3.3947761 -1.0710643
## 52    1.70    coho 3.257091 -1.5570909 -0.4902213
## 70    9.53 chinook 6.314776  3.2152239  1.0139117
## 87    0.90    coho 3.257091 -2.3570909 -0.7430562
## 105   2.61    coho 3.257091 -0.6470909 -0.2035546
## 122  11.82 chinook 6.314776  5.5052239  1.7507263

The histogram of residuals is constructed with geom_histogram() below. Note that the color of the histogram bars are modified and the bin width is set to better control the number of bars in the histogram. Finally, the bottom multiplier for the y-axis is set to zero so that that histogram bars do not “hover” above the x-axis.

ggplot(data=tmp,mapping=aes(x=resids)) +
  geom_histogram(color="gray30",fill="gray70",binwidth=0.5) +
  scale_y_continuous(expand=expansion(mult=c(0,0.05)))

The boxplot of residuals by group (species in this case) is constructed with geom_boxplot() below (again controlling the colors of the boxplot).

ggplot(data=tmp,mapping=aes(x=species,y=resids)) +
  geom_boxplot(color="gray30",fill="gray70")

These plots can be further modified using methods typical for ggplot (see conclusion section).

Two-Way ANOVA

The code below fits a two-way ANOVA model to examine if mean weight differs by species, by year, or by the interaction between species and year.

aov2 <- lm(weight~year*species,data=Mirex)
anova(aov2)

## Analysis of Variance Table
## 
## Response: weight
##               Df Sum Sq Mean Sq F value    Pr(>F)
## year           5 281.86  56.373  6.9954 1.039e-05
## species        1 221.69 221.689 27.5099 7.648e-07
## year:species   5 117.69  23.538  2.9208   0.01628
## Residuals    110 886.44   8.059

residPlot() from FSA (before v0.9.0) shows a boxplot of residuals by each combination of the two factor variables (left) and a histogram of the residuals (right).

FSA::residPlot(aov2)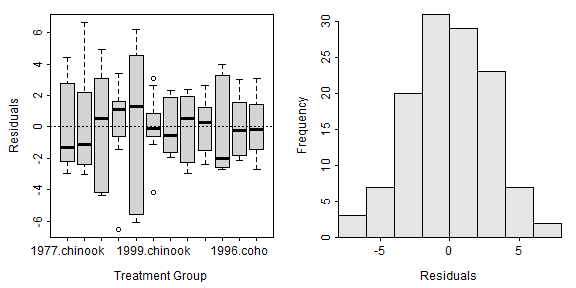

A data.frame of the three variables used in the ANOVA appended with the fitted values and residuals from the model fit must be constructed.

tmp <- dplyr::select(Mirex,weight,species,year) %>%
  dplyr::mutate(fits=fitted(aov2),
                resids=resid(aov2),
                sresids=rstudent(aov2))

The histogram of residuals is constructed exactly as before and won’t be repeated here. The boxplot of residuals by group is constructed with one of the factor variables on the x-axis³ and the other factor variable as separate facets.

ggplot(data=tmp,mapping=aes(x=year,y=resids)) +
  geom_boxplot(color="gray30",fill="gray70") +
  facet_wrap(vars(species))

Simple Linear Regression

The code below fits a simple linear regression for examining the relationship between mirex concentration and salmon weight.

slr <- lm(mirex~weight,data=Mirex)
anova(slr)

## Analysis of Variance Table
## 
## Response: mirex
##            Df  Sum Sq  Mean Sq F value    Pr(>F)
## weight      1 0.22298 0.222980  26.556 1.019e-06
## Residuals 120 1.00758 0.008396

residPlot() from FSA (before v0.9.0) shows a scatterplot of residuals versus fitted values (left) and a histogram of residuals (right).

FSA::residPlot(slr)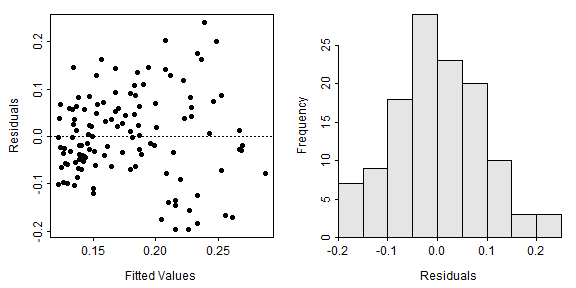

A data.frame of the two variables used in the ANOVA appended with the fitted values and residuals from the model fit must be constructed.

tmp <- dplyr::select(Mirex,weight,mirex) %>%
  dplyr::mutate(fits=fitted(slr),
                resids=resid(slr),
                sresids=rstudent(slr))

The histogram of residuals is constructed exactly as before and won’t be repeated here. The scatterplot of residuals versus fitted values is constructed with geom_point() as below. Note that geom_hline() is used to place the horizontal line at 0 on the y-axis.

ggplot(data=tmp,mapping=aes(x=fits,y=resids)) +
  geom_point() +
  geom_hline(yintercept=0,linetype="dashed")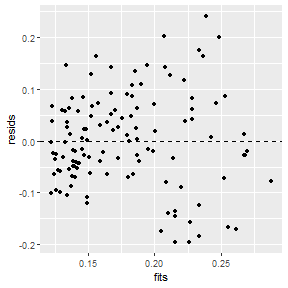

It is also possible to include a loess smoother to help identify a possible nonlinearity in this residual plot.

ggplot(data=tmp,mapping=aes(x=fits,y=resids)) +
  geom_point() +
  geom_hline(yintercept=0,linetype="dashed") +
  geom_smooth()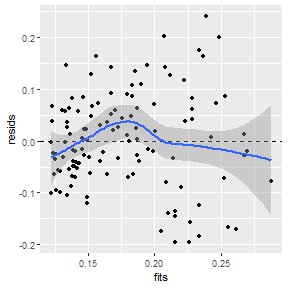

Indicator Variable Regression

The code below fits an indicator variable regression to examine if the relationship between mirex concentration and salmon weight differs betwen species.

ivr <- lm(mirex~weight*species,data=Mirex)
anova(ivr)

## Analysis of Variance Table
## 
## Response: mirex
##                 Df  Sum Sq  Mean Sq F value    Pr(>F)
## weight           1 0.22298 0.222980 26.8586 9.155e-07
## species          1 0.00050 0.000498  0.0600   0.80690
## weight:species   1 0.02744 0.027444  3.3057   0.07158
## Residuals      118 0.97964 0.008302

residPlot() from FSA (before v0.9.0) is the same for an IVR as for an SLR, except that the points on the residual plot (left) has different colors for the different groups.

FSA::residPlot(ivr)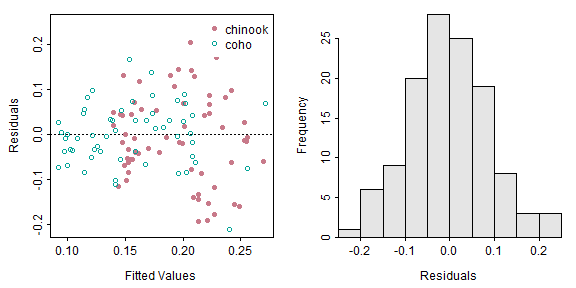

A data.frame of the three variables used in the ANOVA appended with the fitted values and residuals from the model fit must be constructed.

tmp <- dplyr::select(Mirex,weight,mirex,species) %>%
  dplyr::mutate(fits=fitted(ivr),
                resids=resid(ivr),
                sresids=rstudent(ivr))

The histogram of residuals is constructed exactly as before and won’t be repeated here. The scatterplot of residuals versus fitted values is constructed with geom_point(). Note that color= and shape= are both set equal to the factor variable to change the color and plotting character to represent the different groups.

ggplot(data=tmp,mapping=aes(x=fits,y=resids,color=species,shape=species)) +
  geom_point() +
  geom_hline(yintercept=0,linetype="dashed")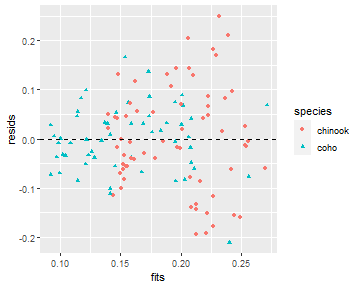

Nonlinear Regression

The following code fits a von Bertalanffy growth function (VBGF) to the total length and age data for spot found in the SpotVA1 data frame built into FSA. Fitting the VBGF is described in more detail here.

vb <- FSA::vbFuns()
vbs <- FSA::vbStarts(tl~age,data=SpotVA1)
nlreg <- nls(tl~vb(age,Linf,K,t0),data=SpotVA1,start=vbs)

residPlot() from FSA (before v0.9.0) produces plots excatly as for a simple linear regression.

FSA::residPlot(nlreg)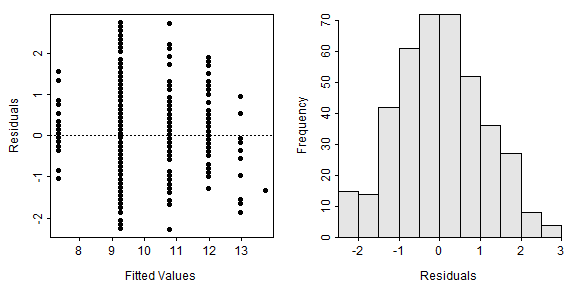

A data.frame of the two variables used in the ANOVA appended with the fitted values and residuals from the model fit must be constructed. The rstudent() function does not work for non-linear models, but the Studentized residuals are computed with nlsResiduals() from nlstools. However, these values are “buried” in the Standardized residuals column of the resi2 matrix returned by that function.

tmp <- dplyr::select(SpotVA1,tl,age) %>%
  dplyr::mutate(fits=fitted(nlreg),
                resids=resid(nlreg),
                sresids=nlstools::nlsResiduals(nlreg)$resi2[,"Standardized residuals"])
peek(tmp,n=8)

##       tl age      fits     resids    sresids
## 1    6.5   0  7.348034 -0.8480343 -0.8051925
## 58   8.3   1  9.251581 -0.9515812 -0.9035082
## 115  8.5   1  9.251581 -0.7515812 -0.7136121
## 173  9.7   1  9.251581  0.4484188  0.4257650
## 230  9.8   2 10.771696 -0.9716957 -0.9226066
## 288 10.5   2 10.771696 -0.2716957 -0.2579700
## 345 11.5   3 11.985613 -0.4856128 -0.4610802
## 403 13.9   4 12.955010  0.9449900  0.8972498

Once this data frame is contstructed the residual plot and histogram of residuals are constructed exactly as before and won’t be repeated here.

Conclusion

The residPlot() function in FSA will be deprecated in v0.9.0 and will likely not exist after that. This post describes a more transparent (i.e., not a “black box”) and flexible set of methods for constructing similar plots using ggplot2 for those who will need to transition away from using residPlot(). It should also be noted that different “residual plot” functionality is available in plot() (from base R when given an object from lm()), car::residualPlots(), DHARMa::plotResiduals(), and ggResidpanel::resid_panel().

As mentioned in the examples above, each plot can be modified further using typical methods for ggplot2. These changes were not illustrated above to minimize the amount of code shown in this post. However, as an example, the code below shows a possible modification of the IVR residual plot shown above. Note that the patchwork package is needed to place the plots side-by-side.

## Recreate the data frame of results for the IVR
tmp <- dplyr::select(Mirex,weight,mirex,species) %>%
  dplyr::mutate(fits=fitted(ivr),
                resids=resid(ivr),
                sresids=rstudent(ivr))

## Create a general theme that can be applied to both plots
theme_DHO <- theme_bw() +
  theme(panel.grid.major=element_line(color="gray90",linetype="dashed"),
        panel.grid.minor=element_blank(),
        axis.title=element_text(size=rel(1.25)),
        axis.text=element_text(size=rel(1.1)),
        legend.position=c(0,1),
        legend.justification=c(-0.05,1.02),
        legend.title=element_blank(),
        legend.text=element_text(size=rel(1.1)))

## Construct the residual plot
r1 <- ggplot(tmp,aes(x=fits,y=sresids,color=species)) +
  geom_point(size=1.5,alpha=0.5) +
  geom_hline(yintercept=0,linetype="dashed") +
  geom_smooth(se=FALSE) +
  scale_y_continuous(name="Studentized Residuals") +
  scale_x_continuous(name="Fitted Values") +
  scale_color_manual(values=c("#E69F00","#0072B2"),guide=FALSE) +
  scale_fill_manual(values=c("#E69F00","#0072B2"),guide=FALSE) +
  theme_DHO

## Construct the histogram of residuals
r2 <- ggplot(tmp,aes(x=sresids,color=species,fill=species)) +
  geom_histogram(alpha=0.5,binwidth=0.25) +
  scale_y_continuous(name="Frequency",expand=expansion(mult=c(0,0.05))) +
  scale_x_continuous(name="Studentized Residuals") +
  scale_color_manual(values=c("#E69F00","#0072B2")) +
  scale_fill_manual(values=c("#E69F00","#0072B2")) +
  theme_DHO

## Put them side-by-side
r1 + r2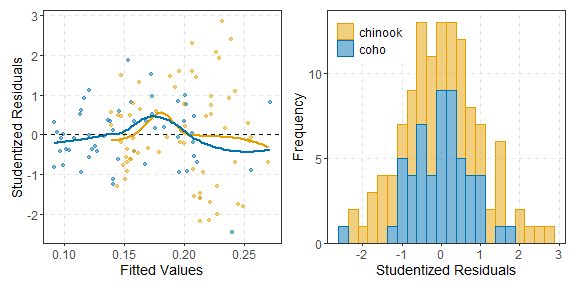

Footnotes