Guest Post Note
Please note that this is a guest post to fishR by Michael Lant, who at the time of this writing is a Senior at Northland College. Thanks, Michael, for the contribution to fishR.
Introduction
My objective is to demonstrate how to create the age bias plots using ggplot2 rather than functions in FSA. Graphs produced in ggplot2 are more flexible than plots from plot() and plotAB() in the FSA package. Below I will show how to use ggplot2 to recreate many of the plots shown in the examples for plot() and plotAB() in FSA.
The code in this post requires functions from the FSA, ggplot2, and dplyr packages.
library(FSA)
library(ggplot2)
library(dplyr)For simplicity I set theme_bw() as the default theme for all plots below. Of course, other themes, including those that you develop, could be used instead.
theme_set(theme_bw())The Data
I will use the WhitefishLC data from FSA. This data.frame contains age readings made by two readers on scales, fin rays, and otoliths, along with consensus readings for each structure.
head(WhitefishLC)#R> fishID tl scale1 scale2 scaleC finray1 finray2 finrayC
#R> 1 1 345 3 3 3 3 3 3
#R> 2 2 334 4 3 4 3 3 3
#R> 3 3 348 7 5 6 3 3 3
#R> 4 4 300 4 3 4 3 2 3
#R> 5 5 330 3 3 3 4 3 4
#R> 6 6 316 4 4 4 2 3 3
#R> otolith1 otolith2 otolithC
#R> 1 3 3 3
#R> 2 3 3 3
#R> 3 3 3 3
#R> 4 3 3 3
#R> 5 3 3 3
#R> 6 6 5 6Additionally, I leverage the results returned by ageBias() from FSA. As described in the documentation, this function computes intermediate and summary statistics for the comparison of paired ages; e.g., between consensus scale and otolith ages below.
ab1 <- ageBias(scaleC~otolithC,data=WhitefishLC,
ref.lab="Otolith Age",nref.lab="Scale Age")The results of ageBias() should be saved to an object. This object has a variety of “data” and “results” in it. For example, the $data object in ab1 contains the original paired age estimates, the differences between those two estimates, and the mean of those two estimates.
head(ab1$data)#R> scaleC otolithC diff mean
#R> 1 3 3 0 3.0
#R> 2 4 3 1 3.5
#R> 3 6 3 3 4.5
#R> 4 4 3 1 3.5
#R> 5 3 3 0 3.0
#R> 6 4 6 -2 5.0In addition, the $bias object of ab1 contains summary statistics of ages for the first structure given in the ageBias() formula by each age of the second structure given in that formula. For example, the first row below gives the number, minimum, maximum, mean, and standard error of the scales ages that were paired with an otolith age of 1. In addition, there is a t-test, adjusted p-value, and a significance statement for testing whether the mean scale age is different from the otolith age. Finally, confidence intervals (defaults to 95%) for the mean scale age at an otolith age of 1 is given, with a statement about whether a confidence interval could be calculated (see the documentation for ageBias() for the criterion used to decide if the confidence interval can be calculated).
head(ab1$bias)#R> otolithC n min max mean SE t adj.p
#R> 1 1 9 1 2 1.444444 0.1756821 2.5298218 0.28212
#R> 2 2 7 1 5 2.000000 0.5773503 0.0000000 1.00000
#R> 3 3 17 1 6 3.352941 0.2416423 1.4605937 0.81743
#R> 4 4 18 2 6 3.833333 0.2322102 -0.7177407 1.00000
#R> 5 5 8 4 8 5.250000 0.4909902 0.5091751 1.00000
#R> 6 6 10 3 6 4.600000 0.2666667 -5.2500003 0.00686
#R> sig LCI UCI canCI
#R> 1 FALSE 1.0393208 1.849568 TRUE
#R> 2 FALSE 0.5872748 3.412725 TRUE
#R> 3 FALSE 2.8406824 3.865200 TRUE
#R> 4 FALSE 3.3434126 4.323254 TRUE
#R> 5 FALSE 4.0889926 6.411007 TRUE
#R> 6 TRUE 3.9967581 5.203242 TRUEThe results in $bias.diff are similar to those for $bias except that the difference in age between the two structures is summarized for each otolith age.
head(ab1$bias.diff)#R> otolithC n min max mean SE t
#R> 1 1 9 0 1 0.4444444 0.1756821 2.5298218
#R> 2 2 7 -1 3 0.0000000 0.5773503 0.0000000
#R> 3 3 17 -2 3 0.3529412 0.2416423 1.4605937
#R> 4 4 18 -2 2 -0.1666667 0.2322102 -0.7177407
#R> 5 5 8 -1 3 0.2500000 0.4909902 0.5091751
#R> 6 6 10 -3 0 -1.4000000 0.2666667 -5.2500003
#R> adj.p sig LCI UCI canCI
#R> 1 0.28212 FALSE 0.03932075 0.8495680 TRUE
#R> 2 1.00000 FALSE -1.41272519 1.4127252 TRUE
#R> 3 0.81743 FALSE -0.15931758 0.8652000 TRUE
#R> 4 1.00000 FALSE -0.65658738 0.3232540 TRUE
#R> 5 1.00000 FALSE -0.91100742 1.4110074 TRUE
#R> 6 0.00686 TRUE -2.00324188 -0.7967581 TRUEThese different data.frames will be used in the ggplot2 code below when creating the various versions of the age-bias plots. Note that at times multiple data frames will be used in the same code so that layers can have different variables.
Basic Age-Bias Plot
Below is the default age-bias plot created by plotAB() in FSA.
FSA::plotAB(ab1)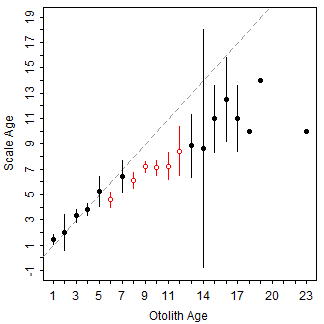
The ggplot2 code below largely recreates this plot.
ggplot(data=ab1$bias) +
geom_abline(slope=1,intercept=0,linetype="dashed",color="gray") +
geom_errorbar(aes(x=otolithC,ymin=LCI,ymax=UCI,color=sig),width=0) +
geom_point(aes(x=otolithC,y=mean,color=sig,fill=sig),shape=21) +
scale_fill_manual(values=c("black","white"),guide="none")+
scale_color_manual(values=c("black","red3"),guide="none") +
scale_x_continuous(name=ab1$ref.lab,breaks=0:25) +
scale_y_continuous(name=ab1$nref.lab,breaks=0:25)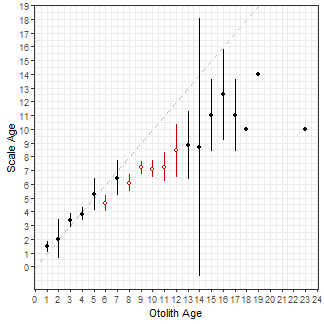
The specifics of the code above is described below.
- The base data used in this plot is the
$biasdata.frame discussed above. - I begin by creating the 45^o^ agreement line (i.e., slope of 1 and intercept of 0) with
geom_abline(), using a dashedlinetype=and a graycolor=. This “layer” is first so that it sits behind the other results. - I then add the error bars using
geom_errorbar(). Theaes()thetics here will map the consensus otolith age to thex=axis and the lower and upper confidence interval values for the mean consensus scale age at each consensus otolith age toymin=andymax=. Thecolor=of the lines are mapped to thesigvariable so that points that are significantly different from the 45^o^ agreement line will have a different color (withscale_color_manual()described below). Finally,width=0assures that the error bars will not have “end caps.” - Points at the mean consensus scale age (
y=) for each otolith age (x=) are then added withgeom_point(). Again, thecolor=andfill=are mapped to thesigvariable so that they will appear different depending on whether the points are significantly different from the 45^o^ agreement line or not. Finally,shape=21represents a point that is an open circle that is outlined with thecolor=color and is filled with thefill=color. scale_fill_manual()andscale_color_manual()are used to set the colors and fills for the levels in thesigvariable. Note thatguide="none"is used so that a legend is not constructed for the colors and fills.scale_x_continuous()andscale_y_continuous()are used to set the labels (withname=) and axis breaks for the x- and y-axes, respectively. The names are drawn from labels that were given in the original call toageBias()and stored inab1.
The gridlines and the size of the fonts could be adjusted by modifying theme, which I did not do here for simplicity.
More Examples
Below are more examples of how ggplot2 can be used to recreate graphs from plot() in FSA. For example, the following plot is very similar to that above, but uses the $bias.diff object in ab1 to plot mean differences between scale and otolith ages against otolith ages. The reference for the differences is a horizontal line at 0 so geom_abline() from above was replaced with geom_hline() here.
ggplot(data=ab1$bias.diff) +
geom_hline(yintercept=0,linetype="dashed",color="gray") +
geom_errorbar(aes(x=otolithC,ymin=LCI,ymax=UCI,color=sig),width=0) +
geom_point(aes(x=otolithC,y=mean,color=sig,fill=sig),shape=21) +
scale_fill_manual(values=c("black","white"),guide="none") +
scale_color_manual(values=c("black","black"),guide="none") +
scale_x_continuous(name=ab1$ref.lab,breaks=0:25) +
scale_y_continuous(name=paste(ab1$nref.lab,"-",ab1$ref.lab),breaks=-15:5)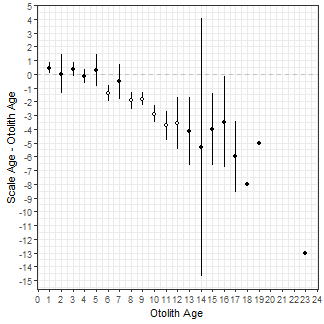
The graph below is similar to above but includes the raw data points from $data and colors the mean (and confidence intervals) for the differences based on the significance as in the first plot. Because data were drawn from different data frames (i.e., ab1$data and ab1$bias.diff) the data= and mapping= arguments had to be moved into the specific geom_s. Note that the raw data were made semi-transparent to emphasize the over-plotting of the discrete ages.
ggplot() +
geom_hline(yintercept=0,linetype="dashed",color="gray") +
geom_point(data=ab1$data,aes(x=otolithC,y=diff),alpha=0.1,size=1.75) +
geom_errorbar(data=ab1$bias.diff,aes(x=otolithC,ymin=LCI,ymax=UCI,color=sig),
width=0) +
geom_point(data=ab1$bias.diff,aes(x=otolithC,y=mean,color=sig,fill=sig),
shape=21,size=1.75) +
scale_fill_manual(values=c("black", "white"),guide="none") +
scale_color_manual(values=c("black","red3"),guide="none") +
scale_x_continuous(name=ab1$ref.lab,breaks=seq(0,25,1)) +
scale_y_continuous(name=paste(ab1$nref.lab,"-",ab1$ref.lab),breaks=-15:5)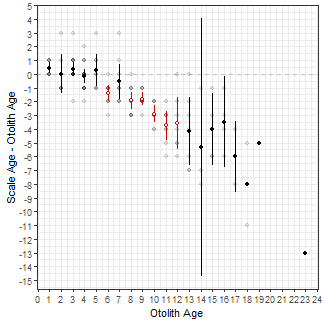
The graph below is the same as above except that a loess smoother has been added with geom_smooth() to emphasize the trend in the differences in ages. The smoother should be fit to the raw data so you must be sure to use ab1$data. I left the default blue color for the smoother and changed the width of the default line slightly by using size=.65.
ggplot() +
geom_hline(yintercept=0,linetype="dashed",color="gray") +
geom_point(data=ab1$data,aes(x=otolithC,y=diff),alpha=0.,size=1.75) +
geom_errorbar(data=ab1$bias.diff,aes(x=otolithC,ymin=LCI,ymax=UCI,color=sig),width=0) +
geom_point(data=ab1$bias.diff,aes(x=otolithC,y=mean,color=sig,fill=sig),shape=21,size=1.75) +
scale_fill_manual(values=c("black", "white"),guide="none") +
scale_color_manual(values=c("black","red3"),guide="none") +
scale_x_continuous(name=ab1$ref.lab,breaks=seq(0,25,1)) +
scale_y_continuous(name=paste(ab1$nref.lab,"-",ab1$ref.lab),breaks=-15:5) +
geom_smooth(data=ab1$data,aes(x=otolithC,y=diff),size=.65)#R> `geom_smooth()` using method = 'loess' and formula 'y ~ x'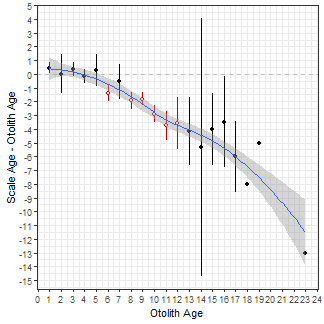
What Prompted This Exploration
Graphics made in ggplot2 are more flexible than the ones produced in FSA. For example, we recently had a user ask if it was possible to make an “age-bias plot” that used “error bars” based on the standard deviation rather than the standard error. While it is questionable whether this is what should be plotted it is nevertheless up to the user and their use case. Because this cannot be done using the plots in FSA we turned to ggplot to make such a graph.
Standard deviation was not returned in any of the ageBias() results (saved in ab1). However, the standard error and sample size were returned in the $bias data frame. The standard deviation can be “back-calculated” from these two values using SD=SE*sqrt(n). I then created two new variables called LSD and USD that are the means minus and plus two standard deviations. All three of these variables are added to the $bias data.frame using mutate() from the dplyr package.
ab1$bias <- ab1$bias %>%
mutate(SD=SE*sqrt(n),
LSD=mean-2*SD,
USD=mean+2*SD)A plot like the very first plot above but using two standard deviations for the error bars is then created by mapping ymin= and ymax= to LSD and USD, respectively, in geom_errorbar(). Note that I removed the color related to the significance test as those don’t pertain to the results when using the standard deviations to represent “error bars.”
ggplot(data = ab1$bias)+
geom_abline(slope=1,intercept=0,linetype="dashed",color="gray") +
geom_errorbar(aes(x=otolithC,ymin=LSD,ymax=USD),width=0) +
geom_point(aes(x=otolithC,y=mean)) +
scale_x_continuous(name =ab1$ref.lab,breaks=0:25) +
scale_y_continuous(name=ab1$nref.lab,breaks=0:25)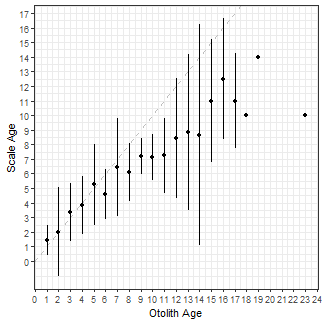
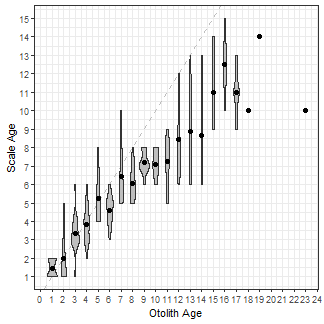
Finally, to demonstrate the flexibility of using ggplot with these type of data, I used a violin plot to show the distribution of scale ages for each otolith age while also highlighting the mean scale age for each otolith age. The violin plots are created with geom_violin() using the raw data stored in $data. The group= must be set to the x-axis variable (i.e., otolith age) so that a separate violin will be constructed for each age on the x-axis. I filled the violins with grey to make them stand out more.
ggplot() +
geom_abline(slope=1,intercept=0,linetype="dashed",color="gray") +
geom_violin(data=WhitefishLC,aes(x=otolithC,y=scaleC,group=otolithC),
fill="grey") +
geom_point(data=ab1$bias,aes(x=otolithC,y=mean),size=2) +
scale_x_continuous(name=ab1$ref.lab,breaks=0:25) +
scale_y_continuous(name=ab1$nref.lab,breaks=0:25)