Alaskan Slimy Sculpin I
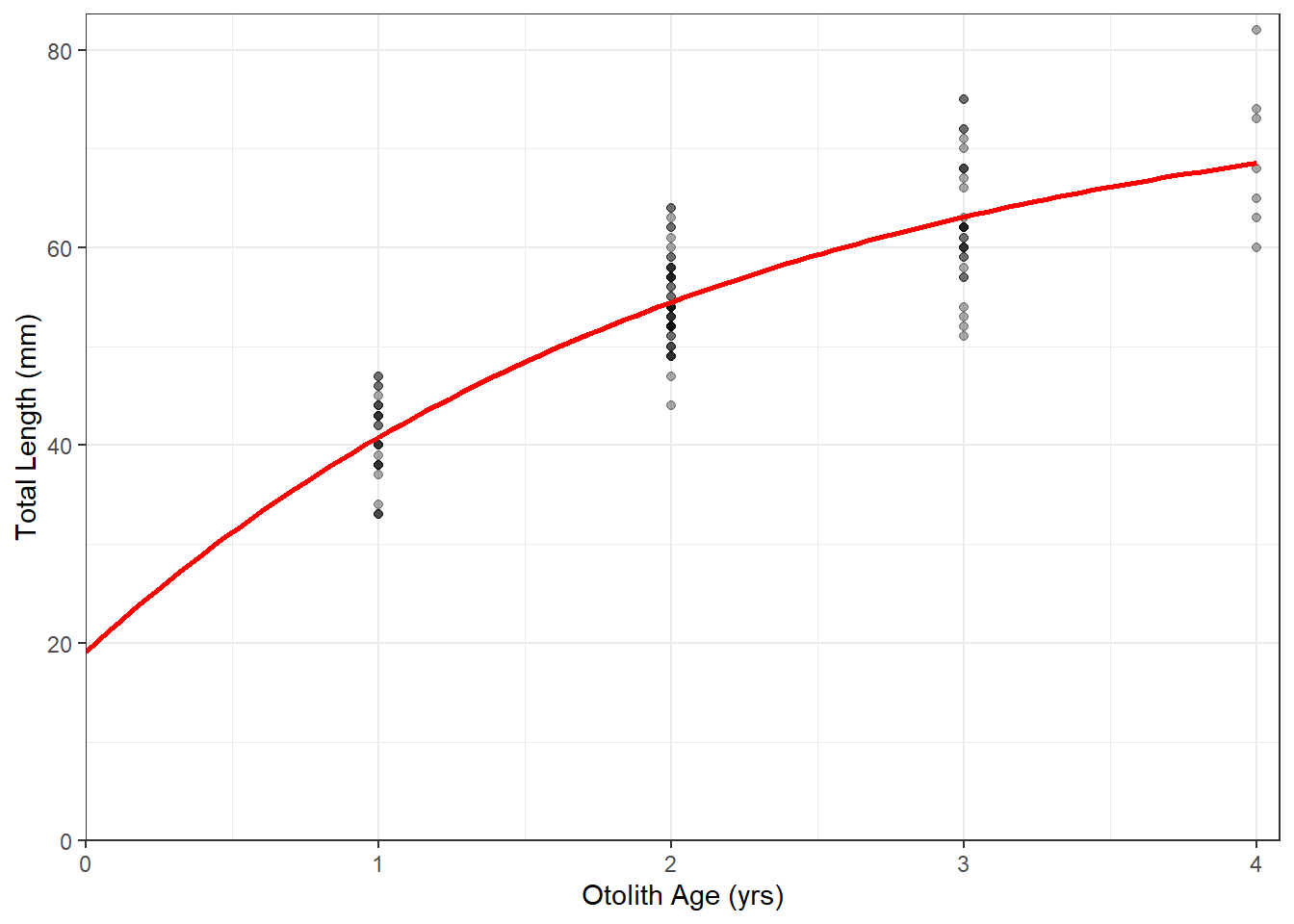
- The plot is shown below. The data show a fairly obvious curve, a fairly obvious asymptote, no fish less than age-1 are shown, and there is considerable variability in length at each age.
- The plot is shown below. The model fits moderately well, but there is considerable variability in length at each age.
- The typical von Bertalanffy equation is \(E(L|t)=77.8(1-e^{-0.46(t+0.61)})\).
- The asymptotic mean length of Slimy Sculpins is 77.8 mm. The Brody growth coefficent, or the rate at which the mean length approaches the asymptotic mean length, is 0.46 year-1. The age at which the mean length is zero (i.e,. the x-intercept) is -0.61 years.
- The 95% confidence interval for the asymptotic mean length is 69.3 to 103.7 mm, for the Brody growth coefficient is 0.22 to 0.73 year-1, and for the x-intercept is -1.37 to -0.17 years. The intervals for the asymptotic mean length and Brody growth coefficient are quite wide because there was considerable variability in length-at-age.
- The predicted mean length at age-3 is 63.1 (with 95% confidence interval from 61.6 to 64.4) mm. This interval is fairly narrow because it is a confidence (rather than prediction) interval and age-3 is a well-represented age in the data.
- Slimy Sculpins will have reached half of their asymptotic length at age 1.50.
R Appendix
library(FSA)
library(tidyverse)
library(nlstools)
sculp <- read.csv("https://raw.githubusercontent.com/droglenc/FSAdata/master/data-raw/SculpinALTER.csv")
vbTyp <- vbFuns("Typical")
ggplot(data=sculp,mapping=aes(x=age,y=tl)) +
geom_point(color=col2rgbt("black",1/3)) +
stat_function(fun=vbTyp,args=list(Linf=coef(fitTyp)),color="red",size=1) +
scale_x_continuous(name="Otolith Age (yrs)",
limits=c(0,NA),expand=expansion(mult=c(0,0.02))) +
scale_y_continuous(name="Total Length (mm)",
limits=c(0,NA),expand=expansion(mult=c(0,0.02))) +
theme_bw()Alaskan Slimy Sculpin II
{:start=“9”} 1. The Gallucci-Quinn von Bertalanffy equation is \(E(L|t)=\frac{35.86}{0.46}(1-e^{-0.46(t--0.61)})\). 1. The growth of Slimy Sculpins near t0 is 35.86 mm/yr. The Brody growth coefficent, or the rate at which the mean length approaches the asymptotic mean length, is 0.46 year-1. The age at which the mean length is zero (i.e,. the x-intercept) is -0.61 years. 1. The common parameter estimates (for K and t0) between the two parameterizations of the von Bertalanffy are the same. This is because a parameterization is the same model, just with different parameters. 1. 35.86=77.8×0.461.
R Appendix
vbGQ <- vbFuns("GallucciQuinn")
svGQ <- vbStarts(tl~age,data=sculp,type="GallucciQuinn")
fitGQ <- nls(tl~vbGQ(age,omega,K,t0),data=sculp,start=svGQ)
bootGQ <- nlsBoot(fitGQ)
estsGQ <- cbind(Est=coef(fitGQ),confint(bootGQ))